Selection Sort:

Selection sort is a basic way to sort a list. It finds the smallest item and puts it at the front until the whole list is sorted in ascending order.

Algorithm Steps:

->Calculate the minimum element
Start with the first element (30) and assume it to be the minimum
Compare it with the rest of the element
Find that 10 is smaller than 30
->Swap the minimum element with the first element in the range
Swap 30 with 10
->Reduce the range
Now, the first element is sorted, so we reduce the range
->Array after one iteration: [10, 50, 40, 20, 30]
->Repeat these steps for the remaining unsorted portion of the array, one element at a time.

Input:30 50 40 20 10

Output:10 20 30 40 50

Selection Sort Code:

#include <bits/stdc++.h> using namespace std; void selectionsort(int arr[], int n){ int min_index; for(int i = 0; i <= n-2; i++){ //Calculate the minimum element min_index = i; for(int j = i; j <= n-1; j++){ if(arr[j] < arr[min_index]){ min_index = j; } } // swap arr[i] and arr[min_index] int temp = arr[i]; arr[i] = arr[min_index]; arr[min_index] = temp; } } int main(){ int n; cin >> n; int arr[n]; for(int i = 0; i < n; i++) cin >> arr[i]; selectionsort(arr,n); for(auto x: arr){ cout << x << " "; } return 0; }

Bubble Sort:

Bubble sort is a basic sorting method for a list of items, where it repeatedly compares and swaps adjacent items to move the larger ones to the end of the list until the entire list is sorted.

Algorithm Steps:

Compare adjacent elements from the start

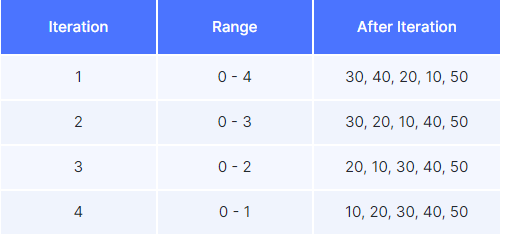
Initial Array: {30, 50, 40, 20, 10}
- Swap 50 and 40 -> {30, 40, 50, 20, 10}
- Swap 50 and 20 -> {30, 40, 20, 50, 10}
- Swap 50 and 10 -> {30, 40, 20, 10, 50}
  
  The largest element (50) has moved to the end
Continue comparing and swapping until fully sorted
- After the 2nd pass: {30, 20, 10, 40, 50} -> {40, 50} sorted
- After the 3rd pass: {20, 10, 30, 40, 50} -> {30, 40, 50} sorted
- After the 4th pass: {10, 20, 30, 40, 50}

The array is now sorted in ascending order using bubble sort

Input:30 50 40 20 10

Output:10 20 30 40 50

Bubble Sort Code:

#include <bits/stdc++.h> using namespace std; void bubblesort(int arr[], int n){ for(int i = n-1; i >= 1; i--) { for(int j = 0; j <= i-1; j++) { if(arr[j] > arr[j+1]) { int temp = arr[j]; arr[j] = arr[j+1]; arr[j+1] = temp; } } } } int main(){ int n; cin >> n; int arr[n]; for(int i = 0; i < n; i++) cin >> arr[i]; bubblesort(arr,n); for(auto x: arr){ cout << x << " "; } return 0; }

Insertion Sort:

Insertion sort is a simple sorting method that divides a list into two parts: a part that’s already sorted and an unsorted part.
It then repeatedly selects an item from the unsorted part and places it in its appropriate position within the sorted part
This continues until the entire list is in the correct order

Algorithm Steps

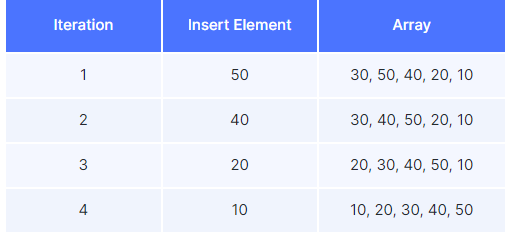
Start with the second element, 50. Compare it with the sorted part
- No Swap between 30 and 50
Move to the next unsorted element, 40, and compare it with the sorted part
- Swap 50 and 40 because 40 is smaller
- Insert 40 in its correct position
Continue with 20:
- Swap 50 and 20 because 20 is smaller
- Swap 40 and 20 because 20 is smaller
- Swap 30 and 20 because 20 is smaller
- Insert 20 where it belongs
Finally, work with 10:
- Swap 50 and 10 because 10 is smaller
- Swap 40 and 10 because 10 is smaller
- Swap 30 and 10 because 10 is smaller
- Swap 20 and 10 because 10 is smaller
- Insert 10 where it belongs

Final sorted array: 10, 20, 30, 40, 50

Input:30 50 40 20 10

Output:10 20 30 40 50

Insertion Sort Code:

#include <bits/stdc++.h>
using namespace std;
void insertionsort(int arr[], int n){
for(int i = 1; i <= n-1; i++){
int j = i;
while((arr[j-1] > arr[j]) && j >= 1){
int temp = arr[j-1];
arr[j-1] = arr[j];
arr[j] = temp;
j–;
}
}
}
int main(){
int n;
cin >> n;
int arr[n];
for(int i = 0; i < n; i++) cin >> arr[i];
insertionsort(arr,n);
for(auto x: arr){
cout << x << ” “;
}
return 0;
}

Merge Sort :

The merge sort algorithm operates by partitioning an array into smaller subarrays, individually sorting these subarrays, and subsequently combining the sorted subarrays to construct the ultimately sorted array. Here’s how the merge sort algorithm works:

Divide: The unsorted list is divided into two equal-sized sublists until each sublist contains only one element. This is done recursively.

Conquer: The individual elements are sorted by comparing and merging them. In the merging step, the two sublists are combined to create a new sorted sublist. This process continues until the entire list is sorted.

Merge: In the merging step, the two sublists are compared, and elements are moved to the new sorted list in the correct order. This process is repeated until all elements from both sublists are included in the sorted list. Here’s a high-level description of the merge sort algorithm:

#include<bits/stdc++.h> using namespace std; void merge(int arr[], int left, int mid, int right) { int i=left; int j = mid+1; int k=0; int n = right-left+1; int new_arr[n]; while(i<=mid and j<=right) { if(arr[i]<arr[j]) { new_arr[k]=arr[i]; i++; k++; } else { new_arr[k]=arr[j]; j++; k++; } } while(i<=mid) { new_arr[k]=arr[i]; i++; k++; } while(j<=right) { new_arr[k]=arr[j]; j++; k++; } for(int c=0;c<=n-1;c++) { arr[left+c]=new_arr[c]; } } void merge_sort(int arr[], int left, int right) { if(left==right) { return; } int mid = (left+right)/2; merge_sort(arr, left, mid); merge_sort(arr, mid+1,right); merge(arr,left,mid,right); } int main() { int n; cin>>n; int arr[n]; for(int i=0;i<n;i++) { cin>>arr[i]; } merge_sort(arr,0,n-1); for(int i=0;i<n;i++) { cout<<arr[i]<<" "; } return 0; }

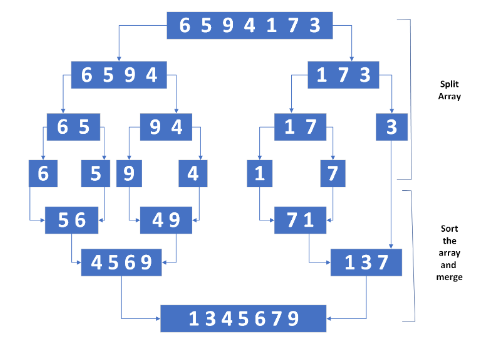
Input:6 5 9 4 1 7 3

Output:1 3 4 5 6 7 9

Quick Sort:

QuickSort is a sorting algorithm that selects an element as a pivot and reorganizes the array by positioning the pivot in its appropriate place within the sorted array.

Quicksort Algorithm:

Choose a Pivot: the pivot is a selected element used to divide the list into two sublists: one with elements smaller than the pivot and one with elements larger. The pivot stays in its final sorted position, and the process is repeated on the sublists until the entire list is sorted. The choice of pivot significantly impacts the algorithm’s efficiency.
Partitioning: Rearrange the elements in the array so that all elements less than the pivot come before it, and all elements greater than the pivot come after it. The pivot itself will be in its final sorted position.
Recursively Sort Sublists: Recursively apply the quicksort algorithm to the two sublists created by the partitioning:
- The left sublist contains elements less than the pivot.
- The right sublist contains elements greater than the pivot.
Combine Sorted Sublists: Once the sublists are sorted, you can combine them with the pivot to get the final sorted array. The left sublist, pivot, and right sublist, in that order, form the fully sorted array.

This process is repeated recursively on the sublists until the entire array is sorted.

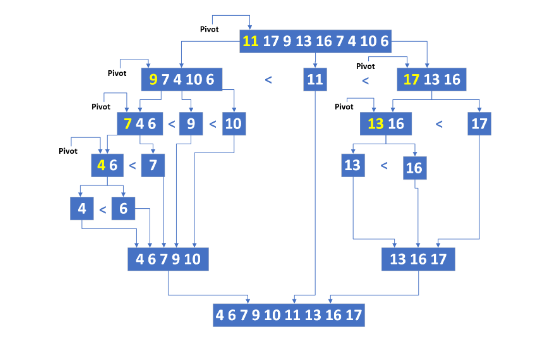
Input:11 17 9 13 16 7 4

Output:4 6 7 9 10 11 13 16 17

Quick Sort Code:

#include<bits/stdc++.h> using namespace std; int partition(int arr[],int low,int high) { int i = low; int j = high; while(i<j) { while(arr[i]<=arr[low] && i<=high-1) { i++; } while(arr[j]>arr[low] && j>=1) { j--; } if(i<j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } int temp = arr[low]; arr[low] = arr[j]; arr[j] = temp; return j; } void quick_Sort(int arr[],int low, int high) { if(low<high) { int j = partition(arr,low,high); quick_Sort(arr,low,j-1); quick_Sort(arr,j+1,high); } } int main() { int n; cin>>n; int arr[n]; for(int i=0;i<n;i++) { cin>>arr[i]; } quick_Sort(arr,0,n-1); for(int i=0;i<n;i++) { cout<<arr[i]<<" "; } return 0; }